來源：Science，研之成理

原文：https://www.science.org/doi/10.1126/science.adg3430

0 背景介紹

熱傳輸可以作為識別不同物態(tài)的指紋。在普通液體中，熱點會擴散，而在超流體中，熱以“第二聲音”波的形式傳播。熱傳輸?shù)闹苯映上駱O具挑戰(zhàn)性，通常會采用檢測次要影響的方法。本研究建立了一個強相互作用原子費米氣體的熱力學分析，其射頻光譜提供了具有亞納開爾分辨率的空間分辨熱測量。超流態(tài)相變被直接觀察到，它從熱擴散突然轉變?yōu)榈诙晜鞑ィ殡S第二聲擴散率的峰值。這種方法可以得到強相互作用費米氣體的全部熱和密度響應，從而得到朗道雙流體流體力學的所有定義屬性。

1 成果掠影

近日，麻省理工學院 Martin W. Zwierlein教授團隊提利用射頻光譜(radiofrequency spectroscopy)繪制出溫度的局部變化。在超流體轉變之上，熱量以擴散方式傳播，而在轉變之下，則觀察到了第二聲的波狀傳播特征。在無量綱費米氣體的超流區(qū)域，第二聲擴散有三個貢獻：熱導率k，剪切粘度h，和從正常超流對流中來的體粘度ζ3。盡管已知對于具有線性色散的純聲子氣體，ζ3 =0，但在T=Tc ? 0:5范圍，正常流體由破壞配對的激發(fā)所主導。在這種情況下，所有三個貢獻的重要性相似。在這個區(qū)域假設ζ3 =0，如參考文獻（27）中所做的那樣，所得結果是無法被證明的，從第一和第二聲擴散單獨獲得粘度和熱導率是不可能的。研究成果以“Thermography of the superfluid transition in a strongly interacting Fermi gas”為題發(fā)表在《Science》。

2 圖文導讀

圖1. 使用射頻光譜直接局部熱成像。

要點：

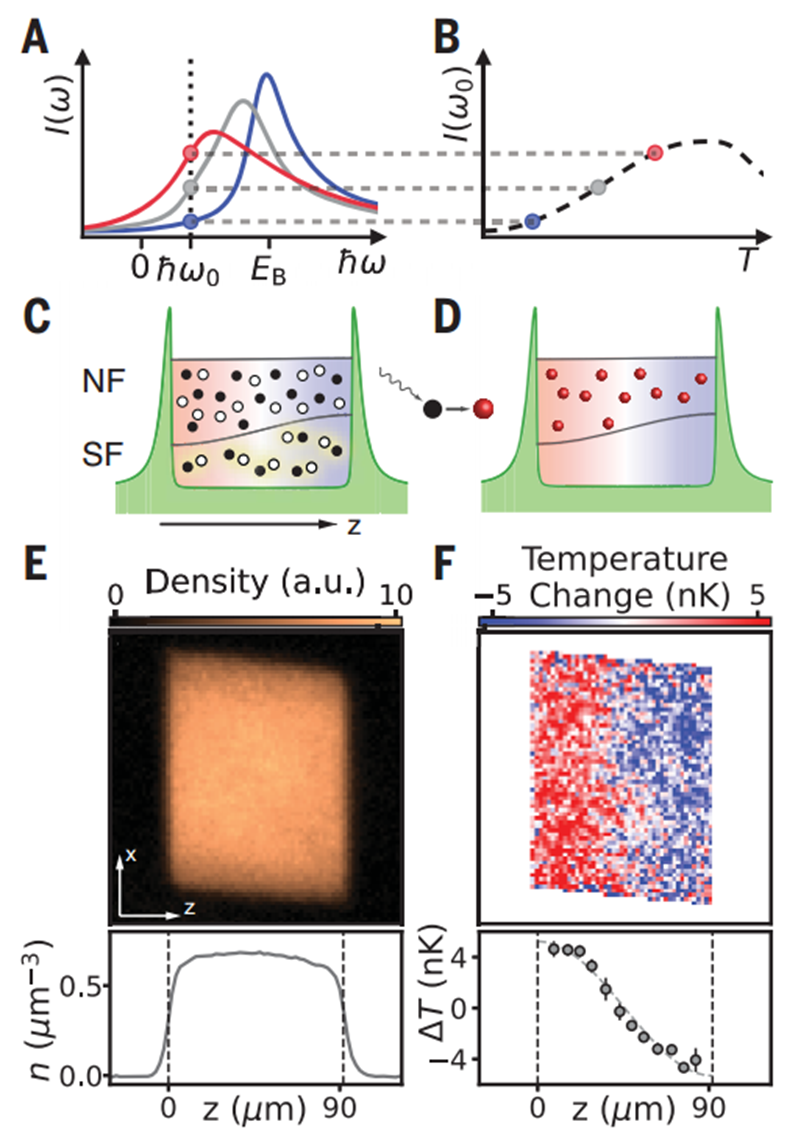
1.本研究提出的方法的工作原理如圖1 A至D所示。在射頻光譜學中，相互作用原子從多體系統(tǒng)中被排出到最初未占據(jù)的內部自旋狀態(tài)中。對于相互作用氣體，得到的光譜依賴于溫度。在高溫下，當熱德布羅意波長小于散射長度和粒子間距時，光譜接近于孤立原子的裸、無偏移響應。相反，在低溫下，光譜顯示出相互作用引起的偏移，稱為“時鐘偏移”。在吸引性二組分費米氣體的特殊情況下，溫度為零時，光譜峰大約會被費米子配對的配對能量EB偏移，而在非零溫度下，破裂的配對會為響應在較低頻率（圖1A）。對于側面譜線上的固定失諧ω0，射頻響應對溫度變化敏感（圖1B）。由于射頻響應可以空間分辨，因此可以通過單幅射頻轉移原子圖像直接測量局部溫度。

2.可以利用這種方法去檢測費米超流體中的第二聲，這是一個激發(fā)氣體中的波，接近Tc時主要由破裂的配對組成（圖1C）。適當調諧的射頻驅動可以從激發(fā)氣體中轉移原子，從而直接、局部地測量熱量（圖1D）。本研究強調，該方法并不依賴于這種簡化的破裂配對圖像，只依賴于射頻光譜的溫度依賴性。因此，它適用于由鐘偏移大小確定的廣泛溫度范圍，對于無量綱費米氣體來說，它們的尺度是費米溫度。

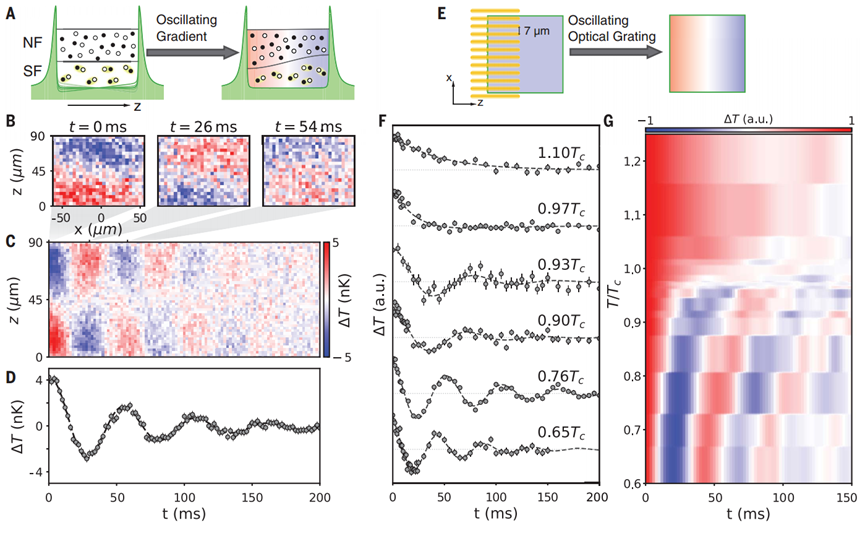
圖2.直接觀察強相互作用費米氣體中熱傳播的超流體轉變。

要點：

1.本研究的實驗從一個均勻的費米超流體開始，被困在一個圓柱形盒狀勢場中，其軸向被定義為z軸，由兩個共振相互作用的費米子（第一（1）和第三（3）超精細態(tài)的6Li）的相等混合物在費舍巴赫共振（磁場690 G）下形成。每個自旋態(tài)的密度為n0 =0.75 mm3，對應于費米能量EF=h·10.5 kHz和費米溫度TF = EF=kB ? 500 nK，其中h是普朗克常數(shù)，kB是玻爾茲曼常數(shù)。

2.為了在超流體氣體中產生溫度梯度，本研究用沿z軸振動的勢梯度共振激發(fā)第二聲的駐波（圖2A）。本研究的熱力學使用射頻從狀態(tài)1轉移原子到最初未占據(jù)的狀態(tài)f ≡ 2。沿徑向（y軸）的一個方向同時進行原位吸收圖像，可以得到原始氣體密度n(x,z)（圖1E），以及從狀態(tài)2轉移的原子密度nf(x,z)攜帶的關于局部溫度的信息（圖1F）。

3.有了對強相互作用費米氣體中溫度進行空間分辨的能力，本研究直接觀察到第二聲作為共振梯度激發(fā)后的自由前后搖擺熱量（圖2B至D）。圖2B顯示了在不同時間t后獲得的測量溫度變化ΔT(x,z,t)。圖2C展示了1D溫度曲線ΔT（z,t）的時間演化，圖2D顯示了由軸向盒長L=91 um支持的第一空間傅里葉模式的振幅的相應演化，所有這些都清楚地證明了熱量的波狀傳播。

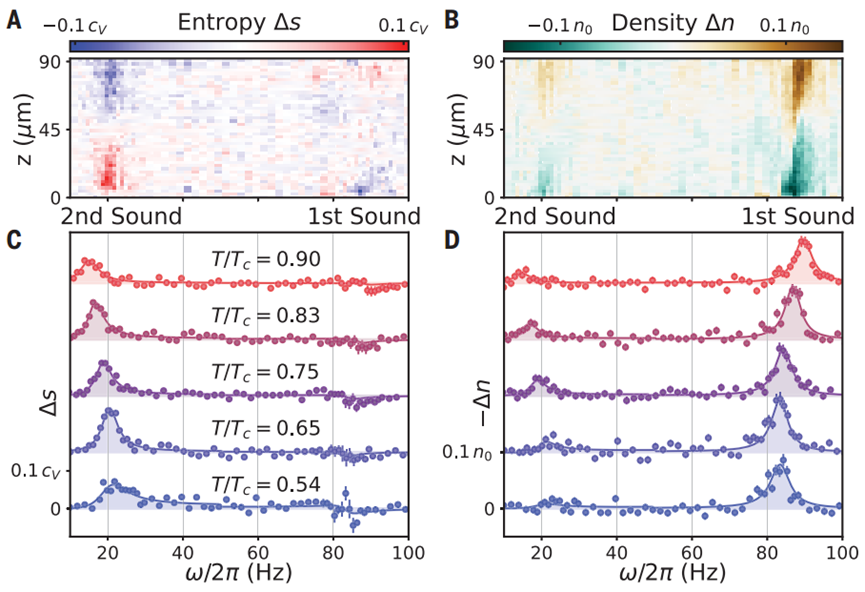
圖3.  無量綱費米超流體的穩(wěn)態(tài)熵和密度響應。

要點：

1.因此，對溫度和密度變化的測量直接產生單位cV下的熵變化。圖3A和B顯示了在僅激發(fā)最低空間模式（j=1）的頻率范圍內，超流體的熵和密度響應。密度顯示出一個主導峰，被歸因于第一聲，在90 Hz附近，以及在20 Hz處微弱的第二聲特征，預期在非零膨脹性氣體中，密度和溫度耦合。然而，在熵通道中，其信號主要來自射頻轉移，強烈的第二聲峰表明有一個很大的響應。

2.在圖3C和D中展示了第一空間傅里葉模式中的熵和密度響應的熱力學演化，它們作為一個直接測量的相位差熵-密度和密度-密度響應函數(shù)。測量的響應函數(shù)完全編碼了關于無量綱費米氣體中的兩流體流體動力學的所有信息。峰值位置和寬度給出了第一聲和第二聲的速度和擴散率。

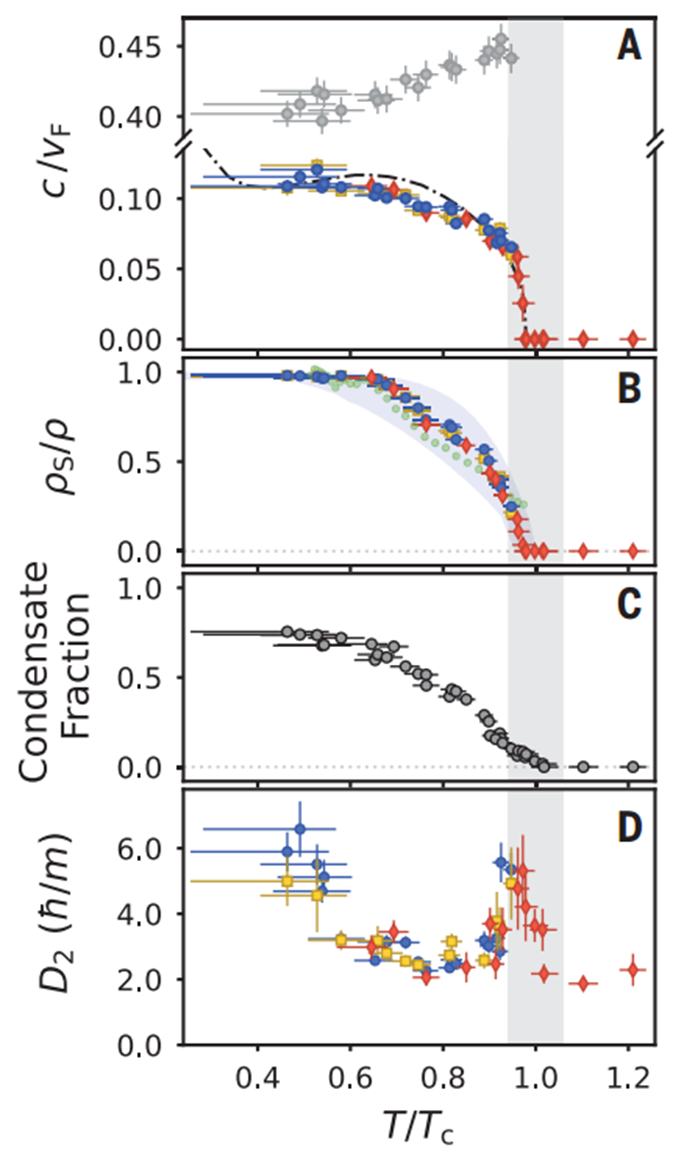
圖4. 第二聲音的速度和擴散率。

要點：

1.圖4A顯示了第二聲速度，與本研究的三種獨立方法一致測量：共振激發(fā)第二聲模式后的自由演化（黃色方塊），局部加熱（紅色鉆石）和穩(wěn)態(tài)響應函數(shù)（藍色圓圈）。超流體分數(shù)是從c2和先前測量的態(tài)方程獲得的，并在圖4B中顯示。測量結果與Nozières和Schmitt-Rink理論（虛線）定性一致，盡管他們的Tc的絕對值與實驗不同。本研究的超流體分數(shù)與在參考文獻中從準1D氣體中的第二聲測量中重建的均勻情況結果相符，該結果依賴于從參考文獻（12）獲得的相同的態(tài)方程。通過局部加熱方法（紅色鉆石），能夠觀察到c2和ρS的連續(xù)演變，從超流相的有限值到正常相的零值。從這次測量中獲得的相變溫度Tc與平衡熱力學測量（垂直灰色區(qū)域）和配對凝聚的發(fā)生一致，本研究也測量了它（圖4C）。

標簽： 導熱散熱 點擊： 評論: