摘要：雙面散熱(Double-sided cooling, DSC)封裝能大幅降低封裝寄生電感和結殼熱阻，提升電氣裝備的功率密度，是SiC 功率模塊的發展趨勢。然而，DSC SiC 功率模塊的失效機理不明、壽命模型缺失，成為制約其商業化應用的關鍵瓶頸，亟待技術突破。傳統加速老化實驗方法的成本較高、耗時較長，不利于產品的快速迭代升級。針對 DSC SiC 功率模塊的可靠性研究，文中提出一種基于有限元的分析方法，基于材料的疲勞老化模型及功率模塊的失效判據，建立DSC SiC 模塊的壽命模型。基于大量功率模塊的壽命測試結果，驗證了有限元模型的可行性和有效性，相對誤差小于 6%。此外，詳細分析SiC和Si功率模塊焊層的應力和蠕變規律，建立不同封裝功率模塊的壽命模型。結果表明：相對于單面散熱封裝，DSC 封裝功率模塊的壽命提升一倍。采用相同封裝，SiC 功率模塊的壽命是 Si 功率模塊壽命的 30%左右。此外，還詳細分析了不同封裝材料對 DSC SiC 功率模塊壽命的影響規律。為下一代DSC SiC功率模塊的研發與應用，提供有益的參考。

關鍵詞：雙面散熱；SiC 功率模塊；可靠性分析；壽命模型

0 引言

隨著晶圓材料和芯片工藝的快速發展，SiC 功率器件的成本持續降低，在國防軍工、電動汽車、新能源等領域，得到廣泛應用。低感、高溫、低熱阻、低成本的 SiC 功率模塊得到持續關注，對功率模塊的封裝結構和封裝工藝提出了更高的要求。相對于單面散熱封裝(Single-sided cooling, SSC)，雙面散熱(Double-sided cooling, DSC)封裝的 SiC 功率模塊，充分利用芯片正面的散熱通道，降低模塊35%的結殼熱阻。此外，DSC 封裝可以消除模塊的鍵合線，減小 80%的封裝寄生電感。可以提高電氣裝備的開關頻率，降低對熱管理的需求，從而提高裝備的功率密度。近年來，日本豐田、日本日立、美國德爾福、中國中車等公司，已經開始探索 DSC SiC 功率模塊的商業化應用。然而，DSC SiC 功率模塊的失效機理、壽命模型等基礎問題，還有待進一步的深入研究。

在 DSC SiC 功率模塊的研究方面，部分文獻研究了功率模塊的優化設計、封裝結構、封裝工藝、壽命模型。在優化設計方面，針對 DSC SiC 功率模塊多物理場之間的相互耦合和相互制約，以封裝結構的尺寸為優化變量，以結殼熱阻、應力應變為優化目標，可以實現熱-力協同的封裝優化設計。

在封裝結構方面，為了進一步降低 DSC SiC 功率模塊的封裝寄生電感，基于磁路相消理論，可以采用P-cell/N-cell 概念，縮短功率回路，減小回路面積。此外，采用先進的封裝結構，譬如：倒裝、3D封裝等，可以有效降低封裝寄生電感。在封裝工藝方面，為了提升 DSC SiC 功率模塊的焊層可靠性，可以采用“低溫焊接、高溫服役”的先進焊接技術，譬如：納米銀燒結、瞬態液相燒結等技術，提升 DSC SiC 功率模塊的可靠性。在壽命模型方面，現有 SSC Si 功率模塊的壽命模型，可以為研究 DSC SiC 功率模塊的壽命模型，提供借鑒。現有功率模塊的壽命模型，普遍采用 Coffin-Manson 模型，表征了熱循環應力與壽命之間的映射規律。

針對鉛焊料在熱循環試驗中的壽命，普遍采用 Norris -Landzberg 模型。隨后，Salmela O 等利用實驗數據對該模型進行了修正，并將其擴展到無鉛焊料。在焊料壽命的基礎上，英飛凌公司提出了 Bayerer模型，計及開通時間、鍵合線電流、鍵合線直徑等諸多影響因素，更詳細地表征功率模塊的壽命。針對新興的無焊料 SKiM 封裝功率模塊，計及鍵合線的影響，賽米控公司提出了改進的壽命模型。

綜上，現有 DSC SiC 功率模塊的研究，目前主要集中在電學、熱學、力學性能的表征與優化，顯示出其低感、低熱阻的技術優勢。然而，DSC SiC 功率模塊的失效模式、失效機理、應力分布規律等基礎研究內容，還鮮有報道。此外，DSC SiC 功率模塊的壽命模型及其影響規律，還是一片空白。

針對 DSC SiC 功率模塊可靠性不明、壽命模型缺失的問題，本文詳細研究 DSC SiC 功率模塊的失效模式、老化規律和壽命模型。基于有限元分析方法，建立功率模塊的可靠性分析模型，并和實驗結果進行校核。基于焊料的疲勞老化模型，建立 DSC SiC 功率模塊的壽命模型，并分析不同封裝材料、封裝結構對功率模塊壽命的影響規律。本文為 DSC SiC 模塊的可靠性研究，提供了新的思路，為 SiC功率模塊的設計研發，提供了新的方法，為 SiC 功率變換器的壽命評估，提供了基礎模型。

1 SSC 和 DSC 功率模塊的結構特點和失效模式

1.1 DSC功率模塊

如圖 1(a)所示，傳統 SSC 封裝的功率模塊為典型的異質集成結構，芯片底面焊接到直接覆銅板(Direct bonding copper, DBC)的上銅層，芯片頂面與上銅層的電氣互連依靠鍵合線完成。芯片產生的熱量通過多層結構傳遞到散熱器，然后耗散到環境中。

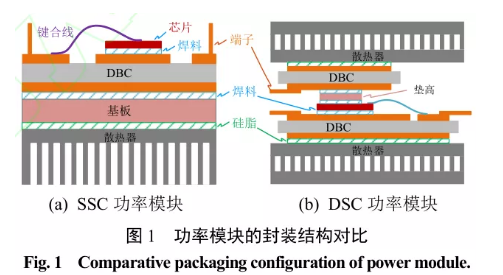
如圖1(b)所示，DSC封裝的功率模塊由2層DBC、墊高、3 層焊料和芯片組成。相對于 SSC 功率模塊，DSC 功率模塊增加了頂面散熱通道，極大地降低功率模塊的結-殼熱阻。芯片功率損耗產生的熱量，同時通過頂部和底部的多層結構，進入散熱器，最終耗散到環境中，提高散熱效率。圖 2 進一步給出了650V 電壓等級 DSC 和 SSC 功率模塊的熱阻對比。功率模塊的熱阻隨著額定電流的增加，指數下降。DSC功率模塊的熱阻比SSC功率模塊減小18%以上。

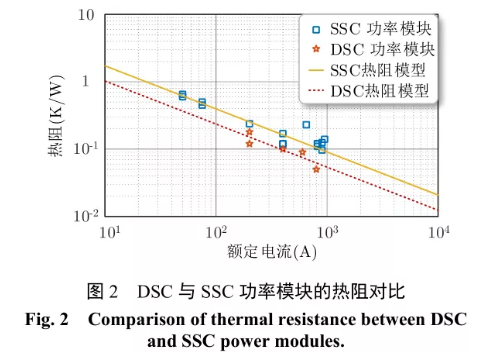
此外，DSC 功率模塊采用頂面的 DBC 代替鍵合線互連，通過優化封裝設計，可以有效降低功率模塊的寄生參數。

經過上述對比，不難發現 DSC 功率模塊在結構上的特點：沒有流過功率回路的鍵合線；增加了芯片上表面的多層結構(即墊片、焊料、DBC)；芯片有 3 層焊料。DSC 功率模塊在結構上的差異，會給可靠性分析帶來較大的差異。

1.2 SSC和DSC 功率模塊的失效模式

功率模塊的疲勞失效直接決定于封裝結構和封裝工藝。在功率模塊內，硅-銅-陶瓷異質層的熱膨脹系數(Thermal expansion coefficient, CTE)和楊氏模量不匹配，在功率循環和溫度循環下，形成功率模塊內的熱-機械應力，在異質層的界面處形成疲勞失效。

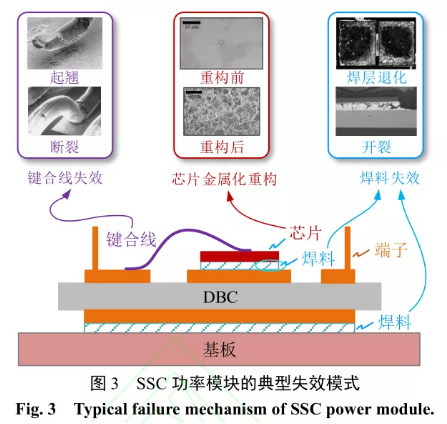
如圖 3 所示，SSC 功率模塊的失效模式主要表現為鍵合線失效、焊料層失效等。由于 DSC功率模塊不存在鍵合線，其失效模式主要為焊料層失效。然而，DSC 功率模塊的失效機理和失效模式還不明晰。尤其是，相對于 SSC 功率模塊的單層焊料，DSC 功率模塊存在三層焊料，其焊層的薄弱環節、失效的先后順序等，都有待進一步深入研究。

DSC 功率模塊仍然采用異質集成結構，可以視為兩個 SSC 功率模塊的疊加。因此，可以借鑒 SSC功率模塊的失效機理和壽命模型，分析 DSC 功率模塊的失效機理，建立其壽命模型。

功率模塊的設計壽命通常為 10 年，為了暴露功率模塊的失效模式，可以采用功率循環等加速老化實驗方法，測試表征功率模塊的壽命。雖然功率循環測試是商業化功率模塊的必需環節，但是功率循環測試周期長、代價高，不適用于功率模塊概念設計階段。如何快速評估模塊的預期壽命，掌握封裝結構和封裝材料對模塊壽命的影響規律，亟待技術突破。

為了適應概念設計階段的技術需求，快速、準確地掌握功率模塊的預期壽命，可以采用多物理場設計方法，結合有限元(Finite element analysis, FEA)模型及其校正技術，建立功率模塊的在線壽命評估模型。然后，采用該模型，預測和評估不同封裝結構和封裝材料對功率模塊壽命的影響規律，快速評估封裝設計的可靠性水平，優化封裝設計的技術路線。

2 SSC 功率模塊壽命的有限元建模及驗證

2.1 SSC 功率模塊的有限元模型

建立功率模塊的壽命模型需要大量的數值計算，在保證精度的前提下，降低模型維度，簡化模型難度，有利于提升計算效率。以焊層疲勞的失效模式為研究對象，以功率模塊的壽命評估為目標，在 COMSOL 多物理場仿真軟件中，建立 SSC 功率模塊的有限元模型。如圖 4 所示，多物理場分析理論表明，二維有限元模型在保證 95%計算精度的前提下，可以提高 10 倍以上的計算速度。因此，為了提高模型的可重復性，在保證足夠計算精度的前提下，將 SSC 功率模塊的三維物理模型，降維為二維有限元模型。

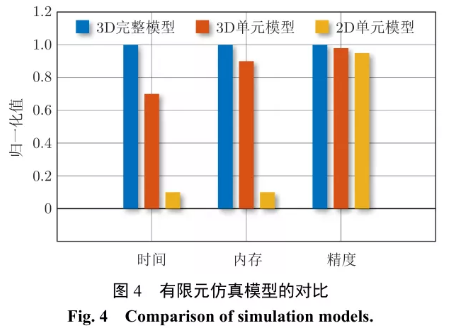
以典型的SSC Si 半橋功率模塊SKM50GB123D為例 ， 采 用 50A/1200V 的 Si IGBT 芯片SIGC41T120R3E，其內部結構如圖 5 所示。在功率模塊內部，芯片之間距離較遠，芯片之間的熱耦合效應可以忽略不計。因此，可以抽取其中的單芯片基本封裝單元，作為研究對象，各層的結構尺寸和材料屬性如表 1 所示。在此基礎上，借助幾何對稱性，可以將 SSC 功率模塊的三維模型轉換為二維模型。

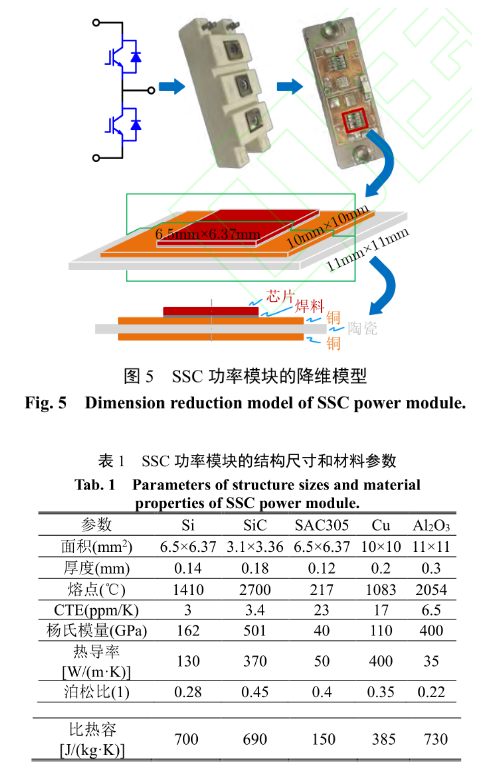
在二維有限元模型的基礎上，需要配置材料的本構模型。從材料力學的角度來看，根據材料的工作溫度和熔點，功率模塊的封裝材料主要分為線彈性材料和粘塑性材料。

半導體、銅和陶瓷材料的工作溫度遠低于其熔點，可以視為線彈性材料。線彈性材料的應力應變規律滿足胡克定律：

其中，σ 和 ε 分別為材料的應力和應變，E 為材料楊氏模量。

然而，焊料的工作溫度約為其熔點的一半，應視為粘塑性材料。焊料內部的蠕變和應力松弛現象非常明顯，應力和應變均為工作溫度和持續時間的函數。粘塑性材料的塑性應變和蠕變規律，可以采用材料的本構方程來表征。對于常用的Anand模型，等效應力 σ 與形變阻抗 s 成正比，即

可見，材料的 Anand 本構模型包含 9 個變量，對于 SAC305 焊料，其模型參數如表 2 所示。

基于圖5 所示的對稱二維模型，邊界條件設置如圖 6 所示。此外，功率芯片設置為特定體積功率密度的熱源，DBC 的底面設置為輥支撐，且散熱條件設置為強迫水冷。模型的左邊界設為對稱邊界，以減小內存；模型的其余邊界均設置為絕熱，且自由移動。

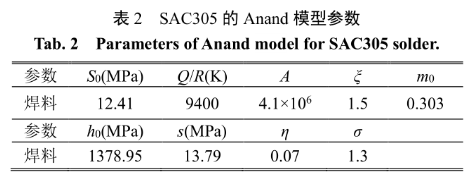
在有限元分析模型中，采用物理壽命模型，評估功率模塊的壽命。在功率芯片上施加方波的功率密度，模擬功率模塊的功率循環實驗。改變方波的幅值和換熱邊界的環境溫度，可以得到功率模塊在不同結溫循環下的溫度、應力、應變規律。結合Anand模型，可以得到焊料的塑性應變和蠕變。為了獲得焊料層應變和壽命之間的映射，可以采用 Morrow 模型

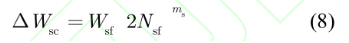
其中，N sf 為焊料層失效前的功率循環周次，ΔWsc 為一次功率循環所累計的蠕變能量，Wsf 和ms分別為材料的疲勞能量系數和疲勞能量指數。對于 SAC305 焊料合金，模型的取值為Wsf = 55×10 6 J/m3 、ms = –0.69。

在實際中，基于應變的 Morrow 模型難于量測。因此，通常所說的壽命模型是指和結溫波動相關的壽命特性。焊層的疲勞老化，引起熱阻的增加，進而導致功率模塊失效。根據焊層失效模型，基于Coffin-Manson 模型，可以得到功率模塊的壽命模型

其中，Nf 為功率模塊的壽命，為功率循環結溫，c1和 c2 分別為功率循環壽命系數。此外，考慮功率循環過程中平均結溫的影響，可以采用 Coffin-Manson-Arrhenius 模型來描述功率模塊的壽命，即

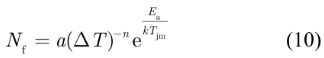
其中，a和n為與初始壽命和結溫波動相關的常數，Ea 為激活能，k = 8.62×10 –5 eV/K 為玻爾茲曼常數，Tjm 為平均結溫。

2.2 功率循環實驗及有限元模型的驗證

典型功率循環實驗的電路原理如圖 7 所示，控制開關采用功率模塊 SKM75GB123D，為了提高測試速度和增強對比參照，將 22 個被測功率模塊串聯測試 [31] 。功率模塊的失效判據定為 20%的結殼熱阻增加。在有限元模型中采用了芯片和封裝一致性，因而可以利用該數據進行實驗驗證。

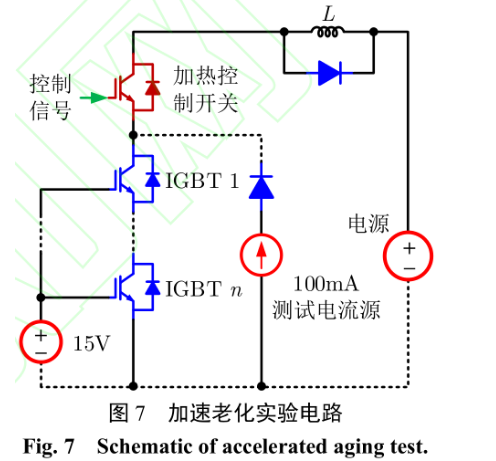
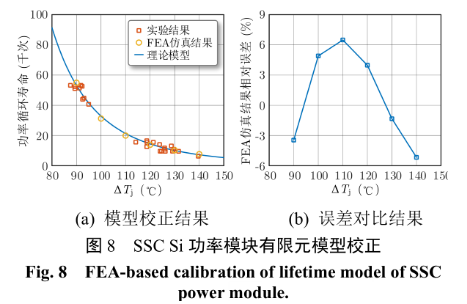
當平均結溫Tjm 為90℃時，設置ΔTj 分別為90℃和 120℃，測試功率模塊的功率循環壽命，實驗結果如圖 8 所示。可以發現，實驗結果與式(9)所示的理論模型吻合較好，辨識得到的功率模塊壽命模型參數為 c1= 5.2×10(12)、c2= 4.2。此外，不同溫度下的有限元仿真結果也與理論的壽命模型相差不大，相對誤差小于 6%。

3 DSC 功率模塊的應力和壽命分布規律

3.1 DSC 功率模塊的有限元模型

基于 SSC 功率模塊的有限元模型，采用實驗結果校驗了該模型對 SSC 功率模塊壽命預測的可行性。這里進一步探索 DSC 功率模塊的有限元模型，以分析 DSC 功率模塊的壽命模型及其影響規律。

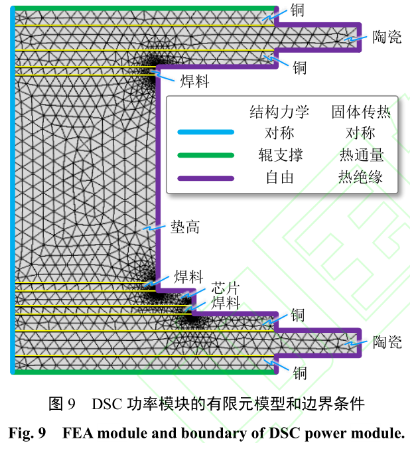
在 DSC 功率模塊的有限元模型中，采用相同尺寸的 IGBT 芯片，進行對比分析，如圖9 所示。芯片底面的封裝材料和封裝尺寸與 SSC 功率模塊完全相同。芯片頂面采用與底面相同的DBC，并在芯片和DBC之間引入了鉬片墊高層，其結構尺寸為 6.0mm×5.7mm×2.5mm，其材料的熱膨脹系數為4.8×10–6 /K、楊氏模量為329GPa 、熱導率為139W/(m·K)。鉬片與芯片的連接，仍采用 0.12mm厚的 SAC305 焊料。

3.2 DSC 功率模塊的失效判據

為了評估功率模塊的壽命，需要確定模塊的失效判據。對于 SSC 功率模塊的失效判據，相對比較成熟。然而，DSC 功率模塊的失效判據還處于探索階段。這里，基于 SSC 功率模塊的失效判據，探索DSC 功率模塊的失效判據。

在功率循環中，非彈性應變能容易在邊角聚集，因而，焊料層邊角處首先開裂失效，導致熱阻增加，最終導致功率模塊失效。對于 SSC 功率模塊，其失效判斷標準通常選為熱阻增加 20%。但是，該失效判據并未指明所對應的焊層失效比例。對于 DSC 功率模塊，其存在三層焊料，各層焊料失效的先后順序，以及對模塊結殼熱阻的影響，都還有待深入研究。

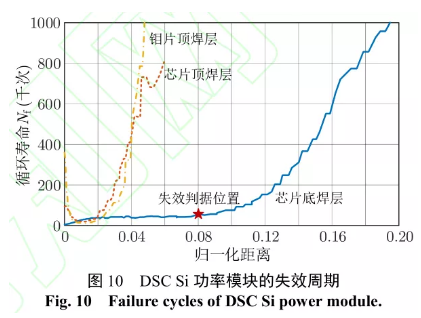
基于圖 9 所示有限元模型，在結溫波動為 ΔTj =120℃的功率循環測試條件下，圖 10 給出了 DSC Si功率模塊的多物理場分析結果。可以發現，鉬片上層焊料、芯片頂層焊料失效約 5%之后，便不再明顯退化，DSC 功率模塊的焊層失效仍然以芯片底層焊料的失效為主。由于場限環的限制，芯片頂面的有效散熱通道減小，且焊料層數更多，并含有墊高層，都會增加頂面封裝結構的厚度和熱阻。因此，芯片的損耗主要通過底面耗散到環境中，芯片底面的熱通量更大，且溫度梯度更高，壽命更短，是DSC 功率模塊的薄弱環節.

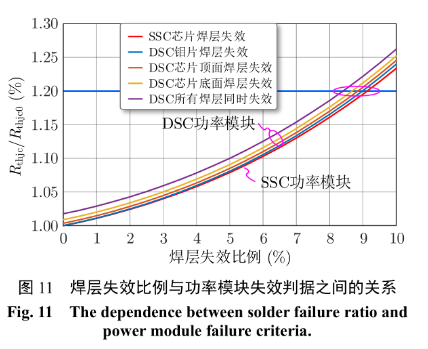
基于圖 9 所示有限元模型，圖 11 進一步給出了各層焊料失效比例對 DSC 功率模塊結殼熱阻的影響規律。可以發現，對于 SSC 功率模塊，當焊料層失效 9%左右，模塊的結殼熱阻增加 20%，即達到SSC功率模塊的失效判據。對于DSC功率模塊，各層焊料失效比例對結殼熱阻的影響規律，與 SSC功率模塊基本一致。因此，可以沿用結殼熱阻增加20%作為 DSC 功率模塊的失效判據。此外，結殼熱阻對芯片底面焊料的失效最為敏感，當底層焊料失效 8%時，可以判定 DSC 功率模塊失效。

3.3 DSC 功率模塊的應力分布規律

功率模塊的應力計算本質是對多層結構的應力分析，忽略了連接層厚度，進行一定的簡化，求解微分方程組，得到異質層交界面的應力分布規律

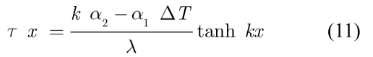
其中，τ 為連接面的剪應力，常數 k 和 λ 為與材料的楊氏模量、厚度等相關的系數，α 為材料的熱膨脹系數，x 為到對稱中心的距離。由式(11)可知，越靠近芯片邊緣，應力越大；材料的熱膨脹系數相差越多，應力越大。相對于有限元方法，數學解析模型能得到一定的規律，并做出一定的物理解釋，但是模型假設過于理想，準確性較差。此外，為了分析功率模塊的蠕變耗散能，評估功率模塊的壽命，有限元分析方法更為方便。因此，本文采用有限元模型來分析功率模塊的熱-力行為。

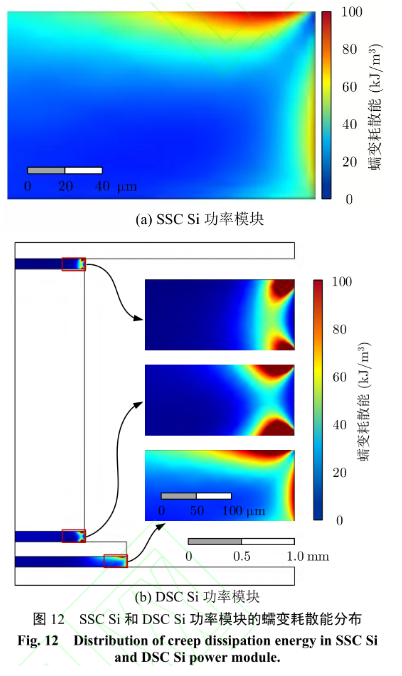
焊料層邊角處是裂紋萌芽地帶，此處的應力和非彈性應變也較為集中。因此，分析焊料層邊角處的應力應變聚集情況，能夠較好地揭示焊料層的失效機理。針對 SSC Si 和 DSC Si 功率模塊，圖 12對比了焊料層的蠕變耗散能分布情況。可以發現：對于 DSC Si 功率模塊，焊料層邊角處的應變聚集區域更小，有利于減緩裂紋的萌發，提升其功率循環壽命。

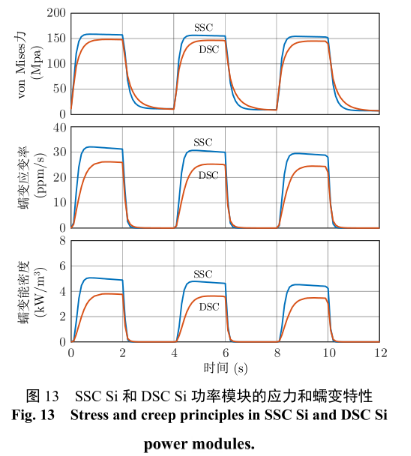
在功率循環過程中，SSC 和 DSC 功率模塊受到的應力應變和蠕變行為有著明顯的差異。以循環溫度ΔTj = 120℃時為例，焊料層的應力和蠕變特性，如圖 13。相對于 SSC 功率模塊，DSC 功率模塊的芯片頂面結構兼具耗散功率和平衡應力的作用，減小芯片焊料層的 5%應力、15%蠕變應變率和 20%蠕變能密度。根據式(8)，單次功率循環所積累的蠕變能量決定是焊料層的疲勞壽命，進而影響功率模塊的功率循環壽命。可見，相對于 SSC 功率模塊，DSC 功率模塊能夠明顯降低焊料層的應力應變，顯著提升其功率循環壽命。

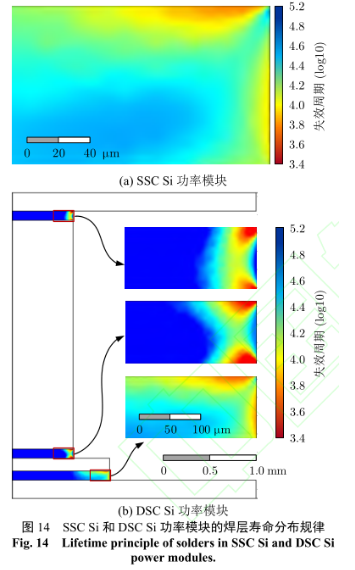
最終，通過有限元分析得到的循環壽命分布如圖 14，與圖 12 和圖 13 所示的應力分析結果基本一致。模塊從焊料層邊角處開始失效，其中 DSC 模塊的失效以芯片底部的焊料層失效為主。頂部兩層焊料在邊角失效后，因為鉬墊片的原因，向內發展得很慢。因此，雙面散熱模塊對器件壽命的提升具有顯著的效果。

4 DSC SiC 功率模塊的壽命模型及影響規律

4.1 DSC SiC 功率模塊的應力行為分析

前述分析表明，采用 DSC 封裝，可以降低 Si功率模塊的熱應力，提升 Si 功率模塊的壽命。這里進一步深入分析 DSC 對 SiC 功率模塊的壽命影響規律。

如表 1 所示，由于材料的性能差異，相對于 Si芯片，SiC 芯片的楊氏模量更大、面積更小，在 DSC功率模塊的模型中，鉬片的大小調整為3mm×2.9mm，其余參數不變。

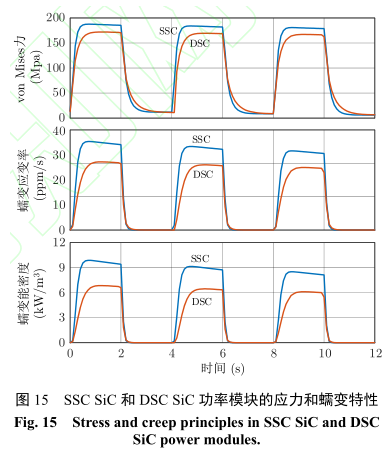
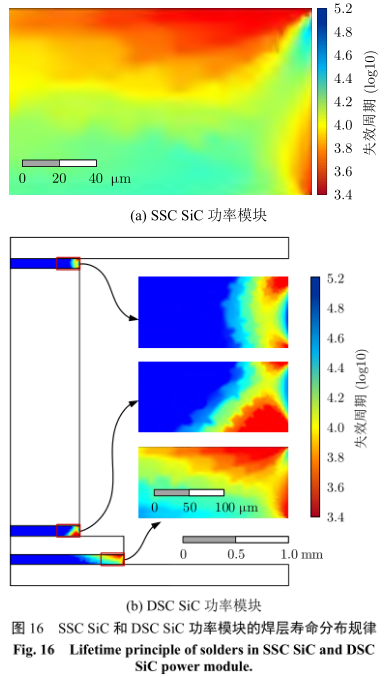
SSC SiC 功率模塊的應力應變更加集中，約是SSC Si 功率模塊的 1.5 倍。但是，采用 DSC 封裝結構，能夠減小 SiC 功率模塊的應力，大幅提升其壽命。SSC SiC 和 DSC SiC 功率模塊的應力和蠕變特性，如圖 15。類似于 Si 功率模塊，相對于 SSC封裝，DSC 封裝能顯著降低 von Mises 力、蠕變應變率和蠕變能密度，提升 SiC 功率模塊的壽命。對比圖 13 和圖 15 可以發現：對于相同的封裝技術，SiC 功率模塊的應力應變仍然大于 Si 功率模塊。因此，相同封裝條件下，SiC 功率模塊的焊料層壽命少于 Si 功率模塊，如圖 16 所示。與 Si 功率模塊類似，相對于 SSC 封裝，DSC 封裝能顯著提升 SiC功率模塊的壽命。

4.2 DSC SiC 功率模塊的壽命模型

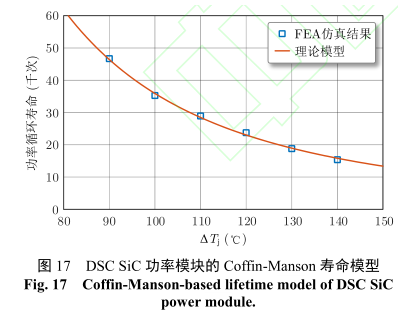
基于前述有限元模型和分析方法，針對 Tjm = 90℃時的有限元分析結果。不同 ΔTj 時，DSC SiC 功率模塊的功率循環壽命，如圖17所示。采用式(9)所示的Coffin-Manson 模型，可以得到DSC SiC功率模塊的壽命模型。模型參數的擬合結果為：c1=2.65×10(9) 、c2 = 2.43。

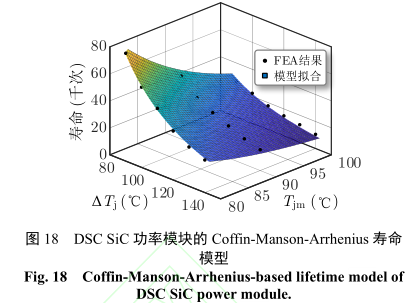
進一步考慮 Tjm 的影響，基于式(10)所示的Coffin-Manson-Arrhenius 模型，圖 18 給出了 DSCSiC 功率模塊的壽命分布規律。當 ΔTj 相同時，Tjm越大，功率模塊的壽命越短；當 Tjm 相同時，ΔTj越大，功率模塊的壽命也越短。此外，有限元分析的結果與式(10)所示模型的預測結果基本一致。辨識得到的模型參數為：a =56.39，n =2.57，Ea =0.57eV。

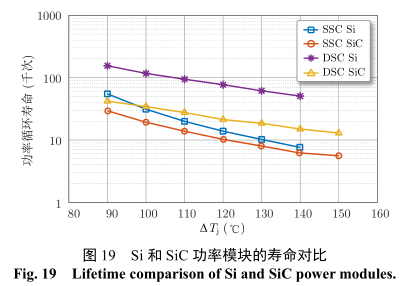
對于 Si 和 SiC 器件，采用 SSC 和 DSC 封裝，當 Tjm = 90℃時，功率模塊的壽命分布規律如圖 19所示。不難發現，SSC SiC 功率模塊的壽命約為 SSCSi 功率模塊壽命的 30%。隨著 ΔTj 增加，二者壽命的差異減小。此外，DSC SiC 功率模塊的壽命是約為 SSC SiC 功率模塊壽命的 2 倍。值得指出的是，相對于 SSC Si 功率模塊，當 ΔTj 較低時，DSC SiC功率模塊的壽命提升效果并不明顯。但是，當 ΔTj較高時，DSC SiC 功率模塊的壽命遠大于 SSC Si功率模塊的壽命。從壽命指標的角度來看，DSC Si功率模塊具有最佳的性能。但是，考慮到高溫、高頻、低損的優異性能，DSC SiC 功率模塊在高功率密度車用電機控制器的應用，具有廣泛的應用前景。可以預見，在更大的 ΔTj 情況下，DSC SiC 功率模塊的優勢會更加明顯。

4.3 封裝材料對DSC SiC 功率模塊壽命的影響

建立功率模塊的壽命模型，可以為功率模塊的概念定型和優化設計，提供基礎理論指導和關鍵技術支撐。

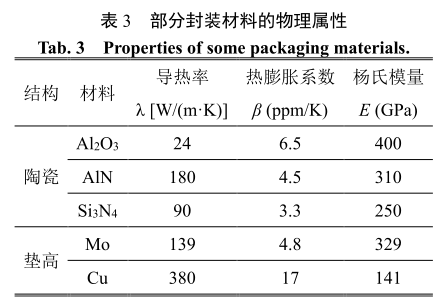
先進的封裝材料有利于降低封裝熱阻，緩解焊層應力，提高功率模塊的壽命。計及 DBC 陶瓷材料和墊高材料的影響，本節深入分析封裝材料對DSC SiC 功率模塊壽命的影響規律，材料的基本屬性如表 3 所示。

基于前述有限元模型和分析方法，不同 DBC陶瓷層材料對 DSC SiC 功率模塊壽命的影響，如圖20 所示。

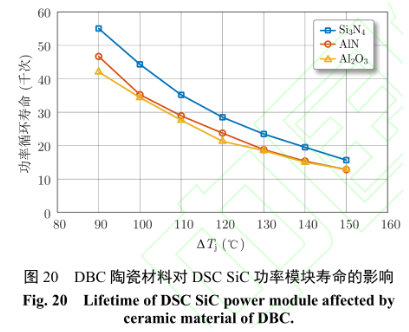
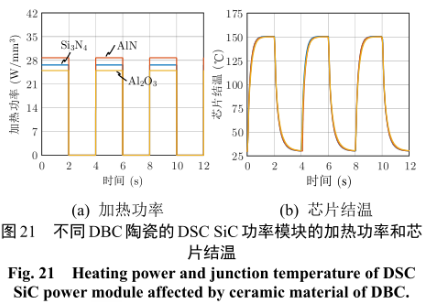
相同ΔTj 條件下，Si3N4功率模塊的可靠性最高，AlN 次之，Al2O3 最差。如表 3 所示，AlN 的熱膨脹系數大于 Si3N4 ，它與 SiC 芯片的熱失配更嚴重。然而，AlN 具有較高的熱導率，有助于降低結-殼熱阻。此外，AlN 的成本比 Si3N4 更低，應用更為廣泛。由于 AlN 的熱導率遠大于 Si3N4和 Al2O3，在相同功率條件下，功率模塊的波動更小，有利于提升功率模塊的壽命，如圖 21。也就是說在相同工作條件下，AlN 的熱阻更小，結溫波動更小，工作壽命將會是更加可觀。

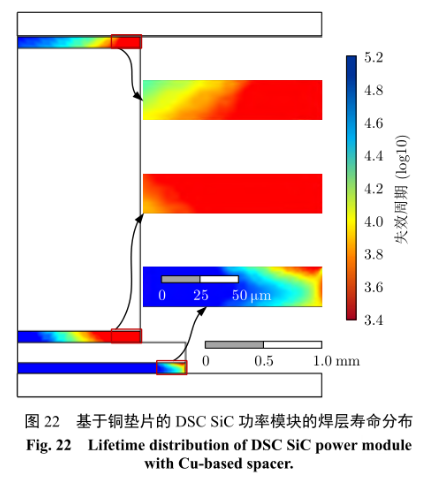
相對于 SSC 封裝，DSC 封裝的墊片覆蓋芯片上表面，直接影響功率模塊的壽命。選用合適的墊片材料，可以緩沖應力，增加 DSC 功率模塊的壽命。若墊片材料選為銅，DSC SiC 功率模塊內的焊料層壽命分布，如圖 22 所示。對比圖 16 所示鉬墊片的結果，可以發現：采用銅墊片后，DSC SiC 功率模塊的焊料急劇失效，且墊片兩側焊料失效最快。雖然，相對于鉬墊片，雖然銅墊片能夠減小結-殼熱阻，但是其熱膨脹系數與 SiC 材料相差更大，熱應力的失配效應更明顯，導致焊層壽命顯著降低。此外，銅墊片的熱阻更小，芯片頂面的熱通量更大，溫度梯度更高，焊料層的溫差更大，進一步加劇焊層失效。

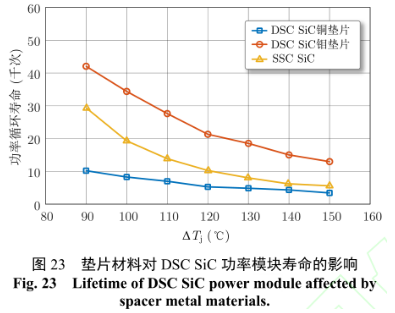
在不同ΔTj 的功率循環條件下，不同封裝的SiC功率模塊的功率循環壽命，如圖 23 所示。隨著 ΔTj的增加，DSC SiC 功率模塊的減小，采用銅墊片后，功率模塊壽命約為鉬墊片的 1/4，其壽命甚至低于SSC SiC 功率模塊。墊片材料的熱膨脹系數，應該接近于 SiC 材料，才能降低模塊的應力，提升模塊的壽命。雖然，銅墊片能夠一定程度上減小 DSC SiC的結殼熱阻，但是其對功率模塊的壽命損耗，遠不如結溫降低帶來的壽命提升。因此，對于 DSC SiC功率模塊，相對于銅墊片，雖然金屬鉬的熱導率稍低，但是鉬墊片仍然是更優的選擇。

5 結論

DSC SiC 功率模塊的是未來功率模塊的重要發展方向，然而現在對它的可靠性分析和壽命模型欠缺。本文通過對功率模塊的簡化降維，得到了一個能快速計算 DSC SiC 循環壽命的 2D 有限元模型，并且利用現有的數據進行間接驗證。針對現階段DSC SiC 功率模塊可靠性測試數據缺乏的問題，本文提出了利用現有的 Si 器件數據進行驗證，為快速獲取 DSC SiC 功率模塊的壽命模型提供了一種新的思路。

本文通過現有的單面散熱功率模塊測試數據，驗證了有限元模型的準確性，并同雙面散熱模塊對比，由此建立了針對雙面散熱模塊的壽命模型。最后，探究了襯板陶瓷材料、墊片材料對模塊壽命的影響，并給出了模塊優化的建議。得到的結論如下：

1)對于 DSC 封裝功率模塊，若采用鉬作為墊高材料，芯片底部焊料層最先失效，且在失效過程中占主導地位。若采用銅作為墊高材料，以墊高層兩側焊料最先失效。

2)雙面散熱模塊的墊片建議采用鉬片，能有效地提升模塊的循環壽命。而采用銅墊片的 DSC 模塊僅為鉬的 1/4。

3)DBC 陶瓷材料建議采用 AlN 或 Si3N4，以有效降低功率模塊的熱阻，提升功率模塊的壽命。

4)采用相同封裝材料，DSC 封裝功率模塊的壽命是 SSC 封裝功率模塊的 2 倍，這種優勢在結溫波動較大的情況更為明顯。

本文來源：知網，原文鏈接：https://kns.cnki.net/kcms/detail/11.2107.tm.20201230.0816.002.html

標簽： 點擊： 評論: